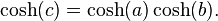Teorema de Pitágoras
| “ |
Em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos. |
” |
Por definição, a
hipotenusa é o lado oposto ao
ângulo reto, e os
catetos
são os dois lados que o formam. O enunciado anterior relaciona
comprimentos, mas o teorema também pode ser enunciado como uma relação
entre áreas:
| “ |
Em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos. |
” |

onde c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados.
O teorema de Pitágoras leva o nome do
matemático grego Pitágoras (570 a.C. – 495 a.C.), que tradicionalmente é creditado pela sua descoberta e
demonstração,
[1][2] embora seja frequentemente argumentado que o conhecimento do teorema seja anterior a ele (há muitas evidências de que
matemáticos babilônicos conheciam
algoritmos
para calcular os lados em casos específicos, mas não se sabe se
conheciam um algoritmo tão geral quanto o teorema de Pitágoras).
[3] [4] [5]
O teorema de Pitágoras é um caso
 O teorema de Pitágoras: a soma das áreas dos quadrados construídos sobre os catetos (a e b) equivale à área do quadrado construído sobre a hipotenusa (c).
O teorema de Pitágoras: a soma das áreas dos quadrados construídos sobre os catetos (a e b) equivale à área do quadrado construído sobre a hipotenusa (c).
Fórmula e corolários
Sendo
c o
comprimento da hipotenusa e
a e
b os comprimentos dos catetos, o teorema pode ser expresso por meio da seguinte equação:

Manipulando algebricamente essa equação, chega-se a que se os
comprimentos de quaisquer dois lados do triângulo retângulo são
conhecidos, o comprimento do terceiro lado pode ser encontrado:
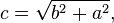
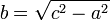 e
e 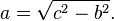
| “ |
Em qualquer triângulo retângulo, a hipotenusa é maior que qualquer um dos catetos, mas menor que a soma deles. [6] |
” |
maior que qualquer um dos catetos pois todos os comprimentos são
necessariamente números positivos, e c² > b², logo c > b, e c²
> a², logo c > a. E a hipotenusa é menor que a soma dos catetos
pois c² = b² + a², e (b+a)² = b² + 2ba + a², logo c² < (b+a)², logo
c < b + a.
 Um triângulo retângulo, de catetos a e b, e de hipotenusa c.
Um triângulo retângulo, de catetos a e b, e de hipotenusa c.
Demonstrações
O teorema de Pitágoras já teve muitas demonstrações publicadas. O livro
The Pythagorean Proposition, de
Elisha Scott Loomis, por exemplo, contém 370 demonstrações diferentes.
[7] Há uma demonstração no livro
Os Elementos, de
Euclides.
[8] E também ofereceram demonstrações, o matemático
indiano Bhaskara Akaria, o
polímata italiano Leonardo da Vinci, e o vigésimo
presidente dos
Estados Unidos,
James A. Garfield.
[9][10][11]
O teorema de Pitágoras é tanto uma afirmação a respeito de áreas quanto
a respeito de comprimentos, algumas provas do teorema são baseadas em
uma dessas interpretações, e outras provas são baseadas na outra
interpretação.
Por comparação de áreas
Não se sabe ao certo qual seria a demonstração utilizada por
Pitágoras, entretanto, muitos autores concordam que ela teria sido feita através da comparação de áreas
, conforme se segue:
- Desenha-se um quadrado de lado
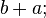
- Traçam-se dois segmentos paralelos aos lados do quadrado;
- Divide-se cada um destes dois retângulos em dois triângulos retos, traçando as diagonais. Chama-se c o comprimento de cada diagonal;
- A área da região formada ao retirar os quatro triângulos retos é igual a

- Desenha-se agora o mesmo quadrado de lado
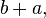 mas colocamos os quatro triângulos retos noutra posição.
mas colocamos os quatro triângulos retos noutra posição.
- A área da região formada quando se retiram os quatro triângulos retos é igual a


Provável forma usada por Pitágoras para demonstrar o teorema que leva seu nome.
Por semelhança de triângulos
Esta demonstração se baseia na
proporcionalidade dos lados de dois triângulos
semelhantes, isto é, que a
razão entre quaisquer dois lados correspondentes de triângulos semelhantes é a mesma, independentemente do tamanho dos triângulos.
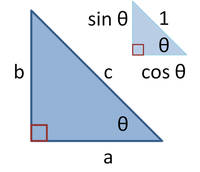
Sendo
ABC um triângulo retângulo, com o ângulo reto localizado em
C, como mostrado na figura. Desenha-se a
altura com origem no ponto
C, e chama-se
H sua intersecção com o lado
AB. O ponto
H divide o comprimento da hipotenusa,
c, nas partes
d e
e. O novo triângulo,
ACH, é
semelhante ao triângulo
ABC, pois ambos tem um ângulo reto, e eles compartilham o ângulo em
A, significando que o terceiro ângulo é o mesmo em ambos os triângulos também,
[12] marcado como
θ na figura. Seguindo-se um raciocínio parecido, percebe-se que o triângulo
CBH também é semelhante à
ABC. A semelhança dos triângulos leva à igualdade das razões dos lados correspondentes:

O primeiro resultado é igual ao
cosseno de cada ângulo
θ e o segundo resultado é igual ao
seno.
Estas relações podem ser escritas como:
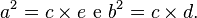
Somando estas duas igualdades, obtém-se
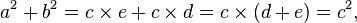
que, rearranjada, é o teorema de Pitágoras:

 Demonstração que utiliza o conceito de semelhança: os triângulos ABC, ACH e CBH têm a mesma forma, diferindo apenas pelas suas posições e tamanhos.
Demonstração que utiliza o conceito de semelhança: os triângulos ABC, ACH e CBH têm a mesma forma, diferindo apenas pelas suas posições e tamanhos.
Demonstração algébrica
A análise da figura da direita permite computar a
área do quadrado
construído sobre a hipotenusa de um triângulo retângulo: ela é quatro
vezes a área desse triângulo mais a área do quadrado restante, de lado (
b−a). Equacionando-se, segue que:
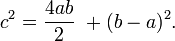
Logo:
 (o termo (b-a)² é um produto notável)
(o termo (b-a)² é um produto notável) (por comutatividade da multiplicação: 2ab = 2ba)
(por comutatividade da multiplicação: 2ab = 2ba)-
 Demonstração algébrica.
Demonstração algébrica.
Por cálculo diferencial
Pode-se chegar ao teorema de Pitágoras pelo estudo de como mudanças
em um lado produzem mudanças na hipotenusa e usando um pouco de
cálculo. É uma demonstração baseada na interpretação métrica do teorema, visto que usa comprimentos, não áreas.
Como resultado da mudança da no lado a,

por semelhança de triângulos e para mudanças diferenciais. Então,

que resulta da adição de um segundo termo para as mudanças no lado b.
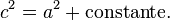
Quando a = 0 então c = b, então a "constante" é b2. Logo,
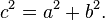
Demonstração que usa equações diferenciais.

Demonstração pelo rearranjo de quatro triângulos retângulos idênticos.
Pelo rearranjo das partes
Uma demonstração por rearranjo é dada pela animação à esquerda. Como
a área total e as áreas dos triângulos são constantes, a área preta
total é constante também. E a área preta pode ser dividida em quadrados
delineados pelos lados a, b, c do triângulo, demonstrando que a2 + b2 = c2.
Na animação à direita, um grande quadrado inicial é formado da área c 2
tornando adjacentes quatro triângulos retângulos idênticos, deixando um
pequeno quadrado no centro do grande quadrado, de modo a acomodar a
diferença de comprimentos dos lados dos triângulos. Dois retângulos são
formados, de lados a e b, movendo-se os triângulos.
Incorporando o pequeno quadrado central com um destes retângulos, os
dois retângulos são feitos em dois quadrados de áreas a 2 e b 2, mostrando que c 2 = a 2 + b 2.
Num espaço com um produto interno
Pode-se estender o
Teorema de Pitágoras a espaços com
produto interno e com uma
norma induzida por este. Nessa situação:
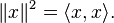
Dois vetores x e y são ditos perpendiculares se:
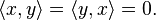
Segue então:
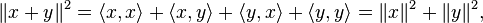

que é o
Teorema de Pitágoras.
Animação mostrando outra demonstração por rearranjo.[13]
Recíproca
- "Para qualquer triângulo com lados l, m, e r, se l² + m² = r², então o ângulo entre l e m mede 90°".
ou, usando apenas palavras,
| “ |
Se num triângulo o quadrado
em um dos lados for igual à soma dos quadrados construídos sobre os
dois lados restantes do triângulo, o ângulo formado pelos dois lados
restantes do triângulo é um ângulo reto. |
” |
Consequências e usos
Talvez nenhuma outra
relação geométrica seja tão utilizada em
matemática
como o teorema de Pitágoras. Ao longo dos séculos foram sendo
registrados muitos problemas curiosos, cujas resoluções têm como base
este famoso teorema
. É possível utilizar o teorema de Pitágoras em todos os
polígonos, pois eles podem ser divididos em
triângulos e esses em triângulos retângulos. E por extensão, a todos os
poliedros.
A diagonal do quadrado
A diagonal do
quadrado divide-o em dois triângulos retângulos
congruentes. Sendo
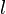
o lado e
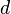
a diagonal, segue que:
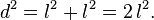

Finalmente, o comprimento da diagonal é encontrado como:

A altura do triângulo equilátero


Finalmente, a altura do triângulo equilátero é encontrado como:
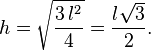
A diagonal do cubo
Seja a a medida de sua aresta (medida de um lado de uma face quadrada)
 (I)
(I)
Também pelo teorema de Pitágoras tem-se que:
 (II)
(II)
De I e II:

Então:

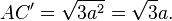
AC' (em azul) é uma diagonal do cubo, enquanto AC (em vermelho) é uma diagonal de uma de suas faces.
Identidade trigonométrica fundamental
-

Disso, segue que:
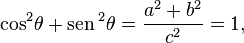
Ternos pitagóricos
-
Um terno pitagórico (trio pitagórico) consiste em três números inteiros positivos a, b, e c, tais que a 2 + b 2 = c 2.
Em outras palavras, um terno pitagórico representa os comprimentos dos
lados de um triângulo retângulo, onde todos os três lados têm
comprimentos inteiros. Essa tripla é geralmente escrita como (a, b, c ). Alguns exemplos bem conhecidos são (3, 4, 5) e (5, 12, 13).
Lista de ternos pitagóricos primitivos até 100:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11,
60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28,
45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65,
72, 97)
Números irracionais como comprimento
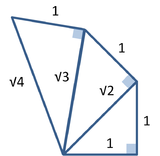 Uma das consequências do teorema de Pitágoras é que comprimentos incomensuráveis (ou seja, cuja razão é um número irracional, tal como a raiz quadrada de 2), podem ser construídos, com instrumentos como régua e compasso. Um triângulo retângulo com ambos os catetos iguais a uma unidade tem uma hipotenusa de comprimento
igual a raiz quadrada de 2. A figura da direita mostra como construir
segmentos de reta com comprimentos iguais a raiz quadrada de qualquer
número inteiro positivo.
Uma das consequências do teorema de Pitágoras é que comprimentos incomensuráveis (ou seja, cuja razão é um número irracional, tal como a raiz quadrada de 2), podem ser construídos, com instrumentos como régua e compasso. Um triângulo retângulo com ambos os catetos iguais a uma unidade tem uma hipotenusa de comprimento
igual a raiz quadrada de 2. A figura da direita mostra como construir
segmentos de reta com comprimentos iguais a raiz quadrada de qualquer
número inteiro positivo.
Distância entre dois pontos
-
Seja

e

Para auxiliar, seja

Então
![d(A,B)=\sqrt[]{d(A,C)^2+d(B,C)^2}=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}.](http://upload.wikimedia.org/wikipedia/pt/math/c/7/5/c756b6f6b267e3037ec6679c8ac47d1b.png)
Generalizações
Lei dos cossenos
-
O teorema de Pitágoras permite calcular um lado de um triângulo retângulo conhecendo os outros dois. A
lei dos cossenos permite calculá-lo em qualquer
triângulo.
Assim, o teorema de Pitágoras é um caso especial do teorema mais geral
que relaciona o comprimento dos lados de qualquer triângulo, a lei dos
cossenos é a seguinte:

onde θ é o ângulo entre os lados a e b. Quando θ é 90 graus, cos(θ) = 0, assim, a fórmula reduz-se ao teorema de Pitágoras.
Teorema de Gua
-
O teorema de Pitágoras pode ser generalizado para um n-simplex
retângulo: o quadrado do (n-1)-volume da hipotenusa é igual à soma dos
quadrados dos (n-1)-volumes dos catetos. Em particular, num tetraedro
retângulo (isto é, que tem 3 faces perpendiculares entre si - os
catetos), o quadrado da área da hipotenusa (a face que não é
perpendicular às restantes) é igual à soma dos quadrados das áreas dos
catetos.
Figuras semelhantes nos três lados
O teorema de Pitágoras foi generalizado por
Euclides em seu livro
Os Elementos para estender-se além das áreas dos quadrados nos três lados, para figuras semelhantes:
[15]
| “ |
Erguendo-se figuras
semelhantes nos lados de um triângulo retângulo, então a soma das áreas
das duas menores é igual à área da maior. |
Na geometria esférica e hiperbólica
O teorema de Pitágoras é derivado dos
axiomas da
geometria euclidiana, e de fato, a versão euclidiana não é válida nas
geometrias não euclidianas. (Foi mostrado que o teorema de Pitágoras é equivalente ao
postulado das paralelas)
Em outras palavras, numa geometria não euclidiana, a relação entre os
lados de um triângulo deve necessariamente tomar outra forma. Por
exemplo, na geometria esférica, a² + b² ≠ c².
Seja
c a hipotenusa de um triângulo rectângulo numa
geometria não euclidiana e
a e
b os catetos. O teorema de Pitágoras toma uma das seguintes formas:

História
A história do teorema pode ser dividida em quatro partes: o conhecimento de
trios pitagóricos, conhecimento da relação entre os lados de um
triângulo retângulo, conhecimento das relações entre ângulos adjacentes, e demonstrações do teorema dentro de sistemas dedutivos.
Há provas que os antigos
babilônios
já conheciam o teorema muito antes de Pitágoras. Tabletes de barro do
período de 1800 a 1600 a.C. foram encontrados e estudados, estando hoje
em vários museus. Um deles, Plimpton 322, mostra uma tabela de 15
linhas e 3 colunas, ilustrando trios pitagóricos.
Na
China, o teorema também já era conhecido cerca de 600 anos antes do período Pitagórico. O problema "Gou Gu", do famoso livro chinês
Zhoubi Saunjing é um exemplo da exitência do Teorema.
[16]

O "triângulo egípcio", de medidas 3, 4, 5, os egípcios usavam uma corda com treze nós equidistantes para construírem ângulos retos.

Ilustração do livro Chou Pei Suan Ching, que sugere uma demonstração do teorema para um triângulo específico (de lados 3, 4 e 5).
Referências
- ↑ George Johnston Allman. Greek Geometry from Thales to Euclid. Reprinted by Kessinger Publishing LLC 2005 ed. [S.l.]: Hodges, Figgis, & Co, 1889. p. 26. ISBN 143260662X
- ↑ Heath, Vol I, p. 144.
- ↑ Otto Neugebauer. The exact sciences in antiquity. Republication of 1957 Brown University Press 2nd ed. [S.l.]: Courier Dover Publications, 1969. p. 36. ISBN 0486223329
- ↑ Mario Livio. The golden ratio: the story of phi, the world's most astonishing number. [S.l.]: Random House, Inc, 2003. p. 25. ISBN 0767908163
- ↑ Pythagoras's theorem in Babylonian mathematics
- ↑ Uma generalização disso é a desigualdade triangular.
- ↑ The Pythagorean Proposition, Classics in Mathematics Education Series. Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Página visitada em 2010-05-04.
- ↑ Euclid's Elements, Book I, Proposition 47
- ↑ Proof #6
- ↑ Proof #16
- ↑ Published in a weekly mathematics column: James A Garfield. (1876). "". The New England Journal of Education 3. as noted in William Dunham. The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities. [S.l.]: Wiley, 1997. p. 96. ISBN 0471176613 and in A calendar of mathematical dates: April 1, 1876 by V. Frederick Rickey
- ↑ Pois a soma dos ângulos internos de qualquer triângulo é sempre igual a 180 graus (32ª proposição de Euclides).
- ↑ Alexander Bogomolny. Pythagorean Theorem, proof number 10. Cut the Knot. Página visitada em 27 February 2010.
- ↑ Demonstração de Euclides no livro Os Elementos
- ↑ Elementos. Livro VI, Proposição VI
- ↑ Proof of Guogu or Pythagoras' Theorem (em inglês)
Ligações externas
«←miinhα αtitudє dєpєndє dα suα!(y)
by:
✪Ќўľė ℛӧѳйήέϔ✪

 http://monografias.brasilescola.com/historia/a-educacao-jovens-adultos-movimento-brasileiro-alfabetizacao.htm
http://monografias.brasilescola.com/historia/a-educacao-jovens-adultos-movimento-brasileiro-alfabetizacao.htm













 6 cm
6 cm










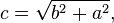
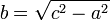 e
e 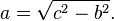

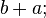

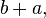 mas colocamos os quatro triângulos retos noutra posição.
mas colocamos os quatro triângulos retos noutra posição.
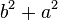 representa a
representa a 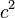 representa a mesma área, então
representa a mesma área, então 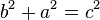 . Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. O segmento de medida c foi chamado de
. Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. O segmento de medida c foi chamado de 

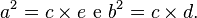
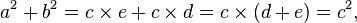


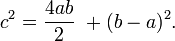
 (o termo (b-a)² é um
(o termo (b-a)² é um  (por
(por 


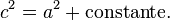
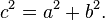


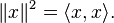
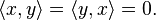
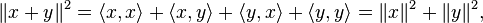

 o lado e
o lado e 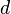 a diagonal, segue que:
a diagonal, segue que: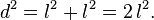



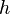 a altura, segue que:
a altura, segue que:

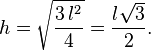
 (I)
(I) (II)
(II)

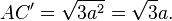

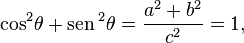

 e
e  Para auxiliar, seja
Para auxiliar, seja 
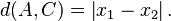
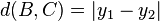
![d(A,B)=\sqrt[]{d(A,C)^2+d(B,C)^2}=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}.](http://upload.wikimedia.org/wikipedia/pt/math/c/7/5/c756b6f6b267e3037ec6679c8ac47d1b.png)